Pythonで数値シミュレーション - 侵略型パーコレーション

はじめに

Pythonは本当に何でもできるので，いろいろな使い方があると思うのですが，僕がどのように使っているのか紹介してみたいと思います．よくつかうパッケージはnumpyです．数値計算のお伴です．これがないと本当に困ります．あとはmatplotlib，scipyです．それからダイアログの表示のためにTkinterを使っています．ここらへんは使っている人も割と多いと思うので，情報も集まりやすいと思います．

ブログの最後に，侵略型パーコレーションクラスターを作成し，そのフラクタル次元を計算するプログラムを丸々載せたいと思います．デフォルトではnumpyとscipy，matplotlibは入っていなかったと思うので，まずそれらを入れておく必要があります．

研究室のノートパソコンに急遽いれることになったとき，

windows7 - Python, SciPy, matplotlibのインストール(Windows) - Qiita:

がめちゃくちゃ便利でした．ありがとうございます，助かりました．

Ubuntuに入れるときは，素直にapt使った方がいいと思います．

下のプログラムのモデルに関しては，自分のレポートのコピペで許してください・・・

侵略型パーコレーションについて

侵略型パーコレーションとして知られている動的な過程は，油を含んだ多孔性の媒体に水を押しこむとき生じる油と水の界面の形をモデル化するのに用いられる．そのアイデアは可能な限り多くの油を回収するために水を用いることにある．この過程では，水のクラスターが最も抵抗の少ない経路を通って油の中に成長していく．L×2Lの格子を考え，初め左側の端が水(侵略者)で占有されているとする．侵略者に対する抵抗の強さは，0と1間の一様乱数で格子の各点に与えられ，侵略の過程の間固定されたままである．すべての侵略者の格子点の最隣接点が周辺の点となる．各分割時間に，最小の乱数を持つ周辺の点が侵略者によって占有され，その点の油(防衛者)は置き換えられる．侵略者のクラスターは格子の左右の端を結ぶ経路が形成されるまで成長する．境界の影響を最小にするために，周期的境界条件が上下の端に対して用いられ，すべての量は格子の中心のL×Lの領域のみについて測定される．関心のある主な量は，侵略者によって占有された格子点の割合と，r+drの間の値の乱数を持つ格子点が占有されている確率P(r)である．

ということで，モデルのイメージを説明したところで，コードの内容に関して触れておきたいと思います．

コードの解説

まず，基本的なところから

格子点はnumpyのarrayを使って行列のようにして表しています（self.latticeと書いてあるところがそれです）．

numpy.random.random([x, y])

でx行y列の行列で，要素が0〜1の乱数の配列ができます．このモデルではそれぞれに与えられた乱数の値が抵抗力を表しているとします．次にwhile節の中で行っていることですが，コメントに書いているように，占有された格子点の周辺の点から，最小の抵抗値をもつ格子点を順に占有していきます．

工夫したところ

# 周辺の点で最も値の小さい格子の座標をmmに
mm = min([(v,k) for k,v in nnsite.items()])[1]

辞書nnsiteのキーと値をnnsite.items()で取り出し，minの仕様である，渡されたタプルの先頭の値の大小を比較することを利用して，値の最小となるキーを取得．

class TopWindow:

    def quit(self):
        self.root.destroy()
        sys.exit()

    def show_window(self, title="title", *args):
        self.root = Tk()
        self.root.title(title)
        frames = []
        for i, arg in enumerate(args):
            frames.append(Frame(self.root, padx=5, pady=5))
            for k, v in arg:
                Button(frames[i],text=k,command=v).pack(expand=YES, fill='x')
            frames[i].pack(fill='x')
        f = Frame(self.root, padx=5, pady=5)
        Button(f,text='quit',command=self.quit).pack(expand=YES, fill='x')
        f.pack(fill='x')
        self.root.mainloop()

引数に与えるタプルの組でボタンのラベルとひも付けされた関数を指定．呼び出すときは

run = (('run', pushed), ('save canvas to sample.eps', pr))
run2 = (('calculate D', b4_pushed),)
top.show_window("Invasion Percolation", run, run2)

のようにする．

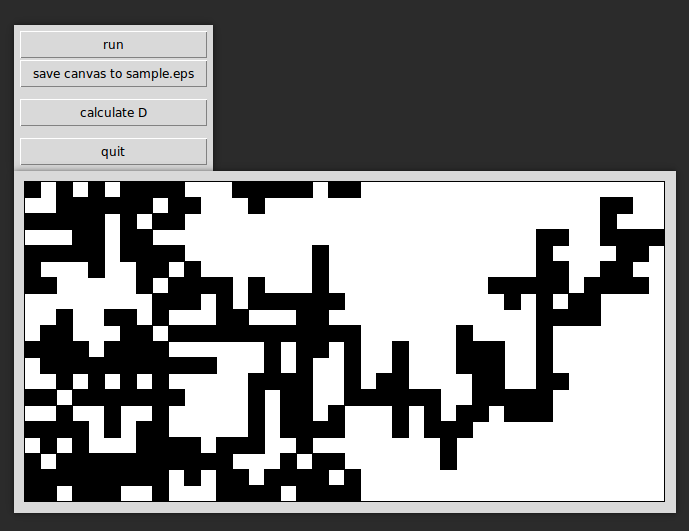
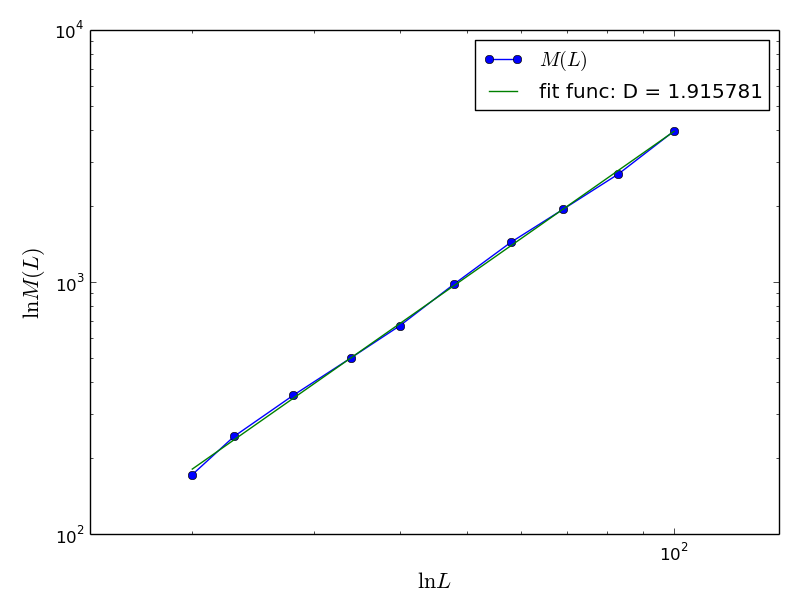
他の細かいところについては，すべて解説できないので，一応シミュレーションの結果どのような画面が得られて，どういった実行結果になるのか紹介します．

このように，ダイアログが表示され，runをクリックするとパーコレーション・クラスターが生成され，calculate_Dで上のようなグラフを得ることができます．その意味などは割愛．

#! /usr/bin/env python
# -*- coding:utf-8 -*-
#
# written by yuzugosho, August 2014.

from Tkinter import *
import sys
import numpy as np
import scipy.optimize as optimize
import matplotlib.pyplot as plt

class Percolation:

    def __init__(self, Lx=40, Ly=20):
        self.sub = None
        self.Lx = Lx
        self.Ly = Ly

    def perc_cluster(self):
        self.lattice = np.random.random([self.Lx+2, self.Ly])
        Lx = self.Lx
        Ly = self.Ly

        # 左端はすべて占有サイト
        self.lattice[:1, :] = 1.5

        self.lattice[Lx+1:, :] = 0
        if self.sub is None or not self.sub.winfo_exists():
            lattice = self.lattice
            ne = [(0, -1), (0, 1), (-1, 0), (1, 0)]

            # 周辺の点の座標を辞書形式で保持する
            nnsite = {(1, y):lattice[1, y] for y in range(Ly)}

            percolate = False
            while len(nnsite) != 0 and percolate == False:

                # 周辺の点で最も値の小さい格子の座標をmmに
                mm = min([(v,k) for k,v in nnsite.items()])[1]

                lattice[mm] = 1
                del nnsite[mm]

                # mmの周辺の点の座標をリストnnに(y方向に周期境界条件を適用)
                nn = [(mm[0] + nx, (mm[1] + ny)%Ly) for nx, ny in ne
                                if lattice[mm[0] + nx, (mm[1] + ny)%Ly] < 1]

                # nnの中で既にnnsiteに含まれているものを除く --> nnlist
                nnlist = list(set(nn) - set(nnsite.keys()))

                # nnsiteに新たな周辺の点を追加する
                for n in nnlist:
                    nnsite[n] = lattice[n]

                # 占有された格子点が右端である時，パーコレートしたと見なす
                if mm[0] == Lx:
                    percolate = True

            self.lattice = lattice[1:-1, :]
        return self.lattice

    def draw_canvas(self, rect, Lx, Ly):
        default_size = 640 # default size of canvas
        r = int(default_size/(2*Lx))
        fig_size_x = 2*r*Lx
        fig_size_y = 2*r*Ly
        margin = 10
        sub = Toplevel()

        sub.title('invasion percolation')
        self.canvas = Canvas(sub, width=fig_size_x+2*margin,
                    height=fig_size_y+2*margin)
        self.canvas.create_rectangle(margin, margin,
                    fig_size_x+margin, fig_size_y+margin,
                    outline='black', fill='white')
        self.canvas.pack()

        c = self.canvas.create_rectangle

        site = np.where(rect==1)
        for m, n in zip(site[0], site[1]):
            c(2*m*r+margin, 2*n*r+margin,
                        2*(m+1)*r+margin, 2*(n+1)*r+margin,
                        outline='black', fill='black')

    def get_fractal_dim(self, trial=20, Lmin=20, Lmax=40, Lsample=10):

        # LminからLmaxの間の整数値で，できるだけlogにしたとき等間隔になるように
        L = np.array([int(i) for i 
                    in np.logspace(np.log10(Lmin), np.log10(Lmax), Lsample)])

        M_L = []
        for l in L:
            self.Lx = l*2
            self.Ly = l
            m_L = 0
            for i in range(trial):
                lattice = self.perc_cluster()

                # 中心のL×L格子中の占有サイト数を合計
                m_L += np.sum(lattice[int(l/2)+1:l+int(l/2),:]==1)

            M_L.append(m_L/float(trial))
            print "L = %d, M_L = %f" % (l, M_L[-1])

        M_L = np.array(M_L)

        def fit_func(parameter0, L, M_L):
            log = np.log
            c1 = parameter0[0]
            c2 = parameter0[1]
            residual = log(M_L) - c1 - c2*log(L)
            return residual

        parameter0 = [0.1, 2.0]
        result = optimize.leastsq(fit_func, parameter0, args=(L, M_L))
        c1 = result[0][0]
        D = result[0][1]
        print "D = %f" % D

        def fitted(L, c1, D):
            return np.exp(c1)*(L**D)

        fig = plt.figure("Fractal Dimension")
        ax = fig.add_subplot(111)
        ax.plot(L, M_L, '-o', label=r"$M(L)$")
        ax.plot(L, fitted(L, c1, D), label="fit func: D = %f" % D)
        ax.set_xlabel(r'$\ln L$', fontsize=16)
        ax.set_ylabel(r'$\ln M(L)$', fontsize=16)
        ax.set_xscale('log')
        ax.set_yscale('log')
        ax.set_ymargin(0.05)
        fig.tight_layout()
        plt.legend(loc='best')
        plt.show()

class TopWindow:

    def quit(self):
        self.root.destroy()
        sys.exit()

    def show_window(self, title="title", *args):
        self.root = Tk()
        self.root.title(title)
        frames = []
        for i, arg in enumerate(args):
            frames.append(Frame(self.root, padx=5, pady=5))
            for k, v in arg:
                Button(frames[i],text=k,command=v).pack(expand=YES, fill='x')
            frames[i].pack(fill='x')
        f = Frame(self.root, padx=5, pady=5)
        Button(f,text='quit',command=self.quit).pack(expand=YES, fill='x')
        f.pack(fill='x')
        self.root.mainloop()

if __name__ == '__main__':
    Lx = 40
    Ly = 20
    top = TopWindow()
    per = Percolation(Lx, Ly)
    count = 1

    def pr():
        global count
        d = per.canvas.postscript(file="figure_%d.eps" % count)
        print "saved the figure to a eps file"
        count += 1

    def pushed():
        per.perc_cluster()
        per.draw_canvas(per.lattice, Lx, Ly)

    def b4_pushed():
        trial = 100; Lmin = 20; Lmax = 100; Lsample = 10
        per.get_fractal_dim(trial, Lmin, Lmax, Lsample)

    run = (('run', pushed), ('save canvas to sample.eps', pr))
    run2 = (('calculate D', b4_pushed),)
    top.show_window("Invasion Percolation", run, run2)